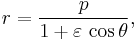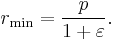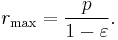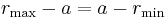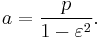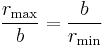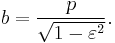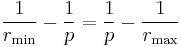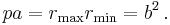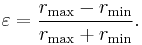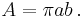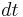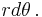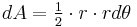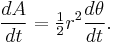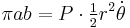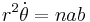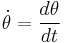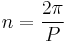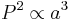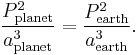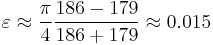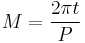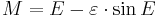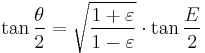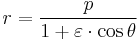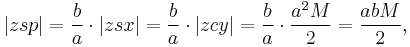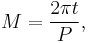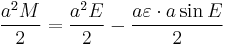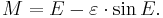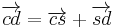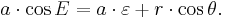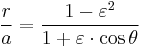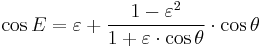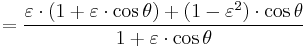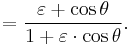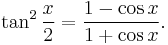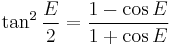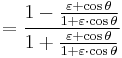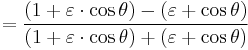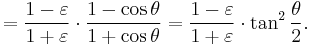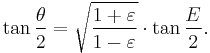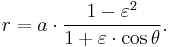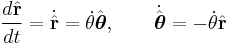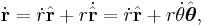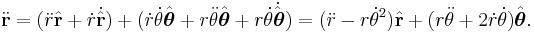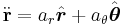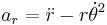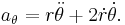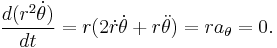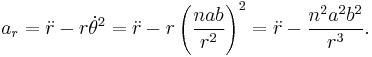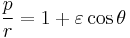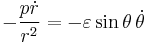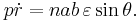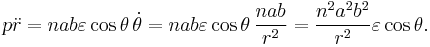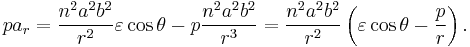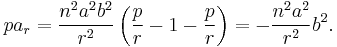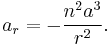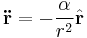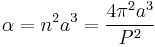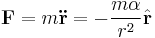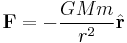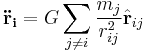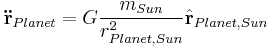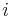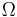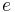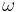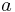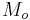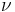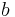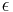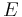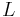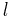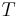Kepler's laws of planetary motion

In astronomy, Kepler's laws give a description of the motion of planets around the Sun.

Kepler's laws are:

The orbit of every planet is an ellipse with the Sun at one of the two foci.
A line joining a planet and the Sun sweeps out equal areas during equal intervals of time.^[1]
The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit.

History

Johannes Kepler published his first two laws in 1609, having found them by analyzing the astronomical observations of Tycho Brahe.^[2] Kepler discovered his third law many years later, and it was published in 1619.^[2] At the time, Kepler's laws were radical claims; the prevailing belief (particularly in epicycle-based theories) was that orbits should be based on perfect circles. Most of the planetary orbits can be rather closely approximated as circles, so it is not immediately evident that the orbits are ellipses. Detailed calculations for the orbit of the planet Mars first indicated to Kepler its elliptical shape, and he inferred that other heavenly bodies, including those farther away from the Sun, have elliptical orbits too. Kepler's laws and his analysis of the observations on which they were based, the assertion that the Earth orbited the Sun, proof that the planets' speeds varied, and use of elliptical orbits rather than circular orbits with epicycles—challenged the long-accepted geocentric models of Aristotle and Ptolemy, and generally supported the heliocentric theory of Nicolaus Copernicus (although Kepler's ellipses likewise did away with Copernicus's circular orbits and epicycles).^[2]

Some eight decades later, Isaac Newton proved that relationships like Kepler's would apply exactly under certain ideal conditions that are to a good approximation fulfilled in the solar system, as consequences of Newton's own laws of motion and law of universal gravitation.^[3]^[4] Because of the nonzero planetary masses and resulting perturbations, Kepler's laws apply only approximately and not exactly to the motions in the solar system.^[3]^[5] Voltaire's Eléments de la philosophie de Newton (Elements of Newton's Philosophy) was in 1738 the first publication to call Kepler's Laws "laws".^[6] Together with Newton's mathematical theories, they are part of the foundation of modern astronomy and physics.^[3]

First Law

See also: ellipse and orbital eccentricity

"The orbit of every planet is an ellipse with the Sun at one of the two foci."

An ellipse is a particular class of mathematical shapes that resemble a stretched out circle. (See the figure to the right.) Note as well that the Sun is not at the center of the ellipse but is at one of the focal points. The other focal point is marked with a lighter dot but is a point that has no physical significance for the orbit. Ellipses have two focal points neither of which is in the center of the ellipse (except for the one special case of the ellipse being a circle). Circles are a special case of an ellipse that are not stretched out and in which both focal points coincide at the center.

How stretched out that ellipse is from a perfect circle is known as its eccentricity; a parameter that varies from 0 (a simple circle) to 1 (an ellipse that is so stretched out that it is a straight line back and forth between the two focal points). The eccentricities of the planets known to Kepler varies from 0.007 (Venus) to 0.2 (Mercury). (See List of planetary objects in the Solar System for more detail.)

After Kepler, though, bodies with highly eccentric orbits have been identified, among them many comets and asteroids. The dwarf planet Pluto was discovered as late as 1929, the delay mostly due to its small size, far distance, and optical faintness. Heavenly bodies such as comets with parabolic or even hyperbolic orbits are possible under the Newtonian theory and have been observed.^[7]

Symbolically an ellipse can be represented in polar coordinates as:

$r=\frac{p}{1%2B\varepsilon\, \cos\theta},$

where (r, θ) are the polar coordinates (from the focus) for the ellipse, p is the semi-latus rectum, and ε is the eccentricity of the ellipse. For a planet orbiting the Sun then r is the distance from the Sun to the planet and θ is the angle with its vertex at the Sun from the location where the planet is closest to the Sun.

At θ = 0°, perihelion, the distance is minimum

$r_\mathrm{min}=\frac{p}{1%2B\varepsilon}.$

At θ = 90° and at θ = 270°, the distance is 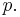$\, p.$

At θ = 180°, aphelion, the distance is maximum

$r_\mathrm{max}=\frac{p}{1-\varepsilon}.$

The semi-major axis a is the arithmetic mean between r_min and r_max:

$\,r_\max - a=a-r_\min$

$a=\frac{p}{1-\varepsilon^2}.$

The semi-minor axis b is the geometric mean between r_min and r_max:

$\frac{r_\max} b =\frac b{r_\min}$

$b=\frac p{\sqrt{1-\varepsilon^2}}.$

The semi-latus rectum p is the harmonic mean between r_min and r_max:

$\frac{1}{r_\min}-\frac{1}{p}=\frac{1}{p}-\frac{1}{r_\max}$

$pa=r_\max r_\min=b^2\,.$

The eccentricity ε is the coefficient of variation between r_min and r_max:

$\varepsilon=\frac{r_\mathrm{max}-r_\mathrm{min}}{r_\mathrm{max}%2Br_\mathrm{min}}.$

The area of the ellipse is

$A=\pi a b\,.$

The special case of a circle is ε = 0, resulting in r = p = r_min = r_max = a = b and A = π r².

Second law

"A line joining a planet and the Sun sweeps out equal areas during equal intervals of time."^[1]

In a small time

$dt\,$

the planet sweeps out a small triangle having base line

$r\,$

and height

$r d\theta\,.$

The area of this triangle is

$dA=\tfrac 1 2\cdot r\cdot r d\theta$

and so the constant areal velocity is

$\frac{dA}{dt}=\tfrac{1}{2}r^2 \frac{d\theta}{dt}.$

Now as the first law states that the planet follows an ellipse, the planet is at different distances from the Sun at different parts in its orbit. So the planet has to move faster when it is closer to the Sun so that it sweeps equal areas in equal times.

The total area enclosed by the elliptical orbit is

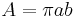$A=\pi ab\,$ .

Therefore the period

$P\,$

satisfies

$\pi ab=P\cdot \tfrac 12r^2 \dot\theta$

$r^2\dot \theta = nab$

where

$\dot\theta=\frac{d\theta}{dt}$

is the angular velocity, (using Newton notation for differentiation), and

$n = \frac{2\pi}{P}$

is the mean motion of the planet around the sun.

Third law

"The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit."

The third law, published by Kepler in 1619 [1] captures the relationship between the distance of planets from the Sun, and their orbital periods. For example, suppose planet A is 4 times as far from the Sun as planet B. Then planet A must traverse 4 times the distance of Planet B each orbit, and moreover it turns out that planet A travels at half the speed of planet B, in order to maintain equilibrium with the reduced gravitational centripetal force due to being 4 times further from the Sun. In total it takes 4×2=8 times as long for planet A to travel an orbit, in agreement with the law (8²=4³).

This third law used to be known as the harmonic law,^[8] because Kepler enunciated it in a laborious attempt to determine what he viewed as the "music of the spheres" according to precise laws, and express it in terms of musical notation.^[9]

This third law currently receives additional attention as it can be used to estimate the distance from an exoplanet to its central star, and help to decide if this distance is inside the habitable zone of that star.^[10]

Symbolically:

$P^2 \propto a^3 \,$

where $P$ is the orbital period of planet and $a$ is the semi-major axis of the orbit.

Interestingly the constant is theoretically same for both-Circular and Elliptical Orbits as well.

The proportionality constant is the same for any planet around the Sun.

$\frac{P_{\rm planet}^2}{a_{\rm planet}^3} = \frac{P_{\rm earth}^2}{a_{\rm earth}^3}.$

So the constant is 1 (sidereal year)²(astronomical unit)⁻³ or 2.97472505×10⁻¹⁹ s²m⁻³. See the actual figures: attributes of major planets.

Generality

These laws approximately describe the motion of any two bodies in orbit around each other. (The statement in the first law about the focus becomes closer to exactitude as one of the masses becomes closer to zero mass. Where there are more than two masses, all of the statements in the laws become closer to exactitude as all except one of the masses become closer to zero mass and as the perturbations then also tend towards zero).^[4] The masses of the two bodies can be nearly equal, e.g. Charon—Pluto (~1:10), in a small proportion, e.g. Moon—Earth (~1:100), or in a great proportion, e.g. Mercury—Sun (~1:10,000,000).

In all cases of two-body motion, rotation is about the barycenter of the two bodies, with neither one having its center of mass exactly at one focus of an ellipse. However, both orbits are ellipses with one focus at the barycenter. When the ratio of masses is large, the barycenter may be deep within the larger object, close to its center of mass. In such a case it may require sophisticated precision measurements to detect the separation of the barycenter from the center of mass of the larger object. But in the case of the planets orbiting the Sun, the largest of them are in mass as much as 1/1047.3486 (Jupiter) and 1/3497.898 (Saturn) of the solar mass,^[11] and so it has long been known that the solar system barycenter can sometimes be outside the body of the Sun, up to about a solar diameter from its center.^[12] Thus Kepler's first law, though not far off as an approximation, does not quite accurately describe the orbits of the planets around the Sun under classical physics.

Zero eccentricity

Kepler's laws refine the model of Copernicus. If the eccentricity of a planetary orbit is zero, then Kepler's laws state:

The planetary orbit is a circle
The Sun is in the center
The speed of the planet in the orbit is constant
The square of the sidereal period is proportionate to the cube of the distance from the Sun.

Actually the eccentricities of the orbits of the six planets known to Copernicus and Kepler are quite small, so this gives excellent approximations to the planetary motions, but Kepler's laws give even better fit to the observations.

Kepler's corrections to the Copernican model are not at all obvious:

The planetary orbit is not a circle, but an ellipse
The Sun is not at the center but at a focal point
Neither the linear speed nor the angular speed of the planet in the orbit is constant, but the area speed is constant.
The square of the sidereal period is proportionate to the cube of the mean between the maximum and minimum distances from the Sun.

The nonzero eccentricity of the orbit of the earth makes the time from the March equinox to the September equinox, around 186 days, unequal to the time from the September equinox to the March equinox, around 179 days. The equator cuts the orbit into two parts having areas in the proportion 186 to 179, while a diameter cuts the orbit into equal parts. So the eccentricity of the orbit of the Earth is approximately

$\varepsilon\approx\frac \pi 4 \frac {186-179}{186%2B179}\approx 0.015$

close to the correct value (0.016710219). (See Earth's orbit). The calculation is correct when the perihelion, the date that the Earth is closest to the Sun, is on a solstice. The current perihelion, near January 4, is fairly close to the solstice on December 21 or 22.

Relation to Newton's laws

Isaac Newton computed in his Philosophiæ Naturalis Principia Mathematica the acceleration of a planet moving according to Kepler's first and second law.

The direction of the acceleration is towards the Sun.
The magnitude of the acceleration is in inverse proportion to the square of the distance from the Sun.

This suggests that the Sun may be the physical cause of the acceleration of planets.

Newton defined the force on a planet to be the product of its mass and the acceleration. (See Newton's laws of motion). So:

Every planet is attracted towards the Sun.
The force on a planet is in direct proportion to the mass of the planet and in inverse proportion to the square of the distance from the Sun.

Here the Sun plays an unsymmetrical part which is unjustified. So he assumed Newton's law of universal gravitation:

All bodies in the solar system attract one another.
The force between two bodies is in direct proportion to their masses and in inverse proportion to the square of the distance between them.

As the planets have small masses compared to that of the Sun, the orbits conform to Kepler's laws approximately. Newton's model improves Kepler's model and gives better fit to the observations. See two-body problem.

A deviation of the motion of a planet from Kepler's laws due to attraction from other planets is called a perturbation.

Computing position as a function of time

Kepler used his two first laws for computing the position of a planet as a function of time. His method involves the solution of a transcendental equation called Kepler's equation.

The procedure for calculating the heliocentric polar coordinates (r,θ) to a planetary position as a function of the time t since perihelion, and the orbital period P, is the following four steps.

1. Compute the mean anomaly M from the formula

$M=\frac{2\pi t}{P}$

2. Compute the eccentric anomaly E by solving Kepler's equation:

$\ M=E-\varepsilon\cdot\sin E$

3. Compute the true anomaly θ by the equation:

$\tan\frac \theta 2 = \sqrt{\frac{1%2B\varepsilon}{1-\varepsilon}}\cdot\tan\frac E 2$

4. Compute the heliocentric distance r from the first law:

$r=\frac p {1%2B\varepsilon\cdot\cos\theta}$

The important special case of circular orbit, ε = 0, gives simply θ = E = M. Because the uniform circular motion was considered to be normal, a deviation from this motion was considered an anomaly.

The proof of this procedure is shown below.

Mean anomaly, M

The Keplerian problem assumes an elliptical orbit and the four points:

s the Sun (at one focus of ellipse);

z the perihelion

c the center of the ellipse

p the planet

and

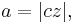$\ a=|cz|,$ distance between center and perihelion, the semimajor axis,

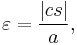$\ \varepsilon={|cs|\over a},$ the eccentricity,

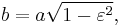$\ b=a\sqrt{1-\varepsilon^2},$ the semiminor axis,

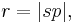$\ r=|sp| ,$ the distance between Sun and planet.

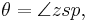$\theta=\angle zsp,$ the direction to the planet as seen from the Sun, the true anomaly.

The problem is to compute the polar coordinates (r,θ) of the planet from the time since perihelion, t.

It is solved in steps. Kepler considered the circle with the major axis as a diameter, and

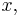$\ x,$ the projection of the planet to the auxiliary circle

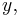$\ y,$ the point on the circle such that the sector areas |zcy| and |zsx| are equal,

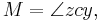$M=\angle zcy,$ the mean anomaly.

The sector areas are related by 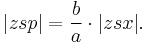$|zsp|=\frac b a \cdot|zsx|.$

The circular sector area 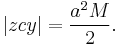$\ |zcy| = \frac{a^2 M}2.$

The area swept since perihelion,

$|zsp|=\frac b a \cdot|zsx|=\frac b a \cdot|zcy|=\frac b a\cdot\frac{a^2 M}2 = \frac {a b M}{2},$

is by Kepler's second law proportional to time since perihelion. So the mean anomaly, M, is proportional to time since perihelion, t.

$M={2 \pi t \over P},$

where P is the orbital period.

Eccentric anomaly, E

When the mean anomaly M is computed, the goal is to compute the true anomaly θ. The function θ=f(M) is, however, not elementary. Kepler's solution is to use

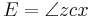$E=\angle zcx$ , x as seen from the centre, the eccentric anomaly

as an intermediate variable, and first compute E as a function of M by solving Kepler's equation below, and then compute the true anomaly θ from the eccentric anomaly E. Here are the details.

$\ |zcy|=|zsx|=|zcx|-|scx|$

$\frac{a^2 M}2=\frac{a^2 E}2-\frac {a\varepsilon\cdot a\sin E}2$

Division by a²/2 gives Kepler's equation

$M=E-\varepsilon\cdot\sin E.$

This equation gives M as a function of E. Determining E for a given M is the inverse problem. Iterative numerical algorithms are commonly used.

Having computed the eccentric anomaly E, the next step is to calculate the true anomaly θ.

True anomaly, θ

Note from the figure that

$\overrightarrow{cd}=\overrightarrow{cs}%2B\overrightarrow{sd}$

so that

$a\cdot\cos E=a\cdot\varepsilon%2Br\cdot\cos \theta.$

Dividing by $a$ and inserting from Kepler's first law

$\ \frac r a =\frac{1-\varepsilon^2}{1%2B\varepsilon\cdot\cos \theta}$

to get

$\cos E =\varepsilon%2B\frac{1-\varepsilon^2}{1%2B\varepsilon\cdot\cos \theta}\cdot\cos \theta$ $=\frac{\varepsilon\cdot(1%2B\varepsilon\cdot\cos \theta)%2B(1-\varepsilon^2)\cdot\cos \theta}{1%2B\varepsilon\cdot\cos \theta}$ $=\frac{\varepsilon %2B\cos \theta}{1%2B\varepsilon\cdot\cos \theta}.$

The result is a usable relationship between the eccentric anomaly E and the true anomaly θ.

A computationally more convenient form follows by substituting into the trigonometric identity:

$\tan^2\frac{x}{2}=\frac{1-\cos x}{1%2B\cos x}.$

Get

$\tan^2\frac{E}{2} =\frac{1-\cos E}{1%2B\cos E}$ $=\frac{1-\frac{\varepsilon%2B\cos \theta}{1%2B\varepsilon\cdot\cos \theta}}{1%2B\frac{\varepsilon%2B\cos \theta}{1%2B\varepsilon\cdot\cos \theta}}$ $=\frac{(1%2B\varepsilon\cdot\cos \theta)-(\varepsilon%2B\cos \theta)}{(1%2B\varepsilon\cdot\cos \theta)%2B(\varepsilon%2B\cos \theta)}$ $=\frac{1-\varepsilon}{1%2B\varepsilon}\cdot\frac{1-\cos \theta}{1%2B\cos \theta}=\frac{1-\varepsilon}{1%2B\varepsilon}\cdot\tan^2\frac{\theta}{2}.$

Multiplying by (1+ε)/(1−ε) and taking the square root gives the result

$\tan\frac \theta2=\sqrt\frac{1%2B\varepsilon}{1-\varepsilon}\cdot\tan\frac E2.$

We have now completed the third step in the connection between time and position in the orbit.

One could even develop a series computing θ directly from M. [2]

Distance, r

The fourth step is to compute the heliocentric distance r from the true anomaly θ by Kepler's first law:

$\ r=a\cdot\frac{1-\varepsilon^2}{1%2B\varepsilon\cdot\cos \theta}.$

Computing the planetary acceleration

In his Principia Mathematica Philosophiae Naturalis, Newton showed that Kepler's laws imply that the acceleration of the planets are directed towards the sun and depend on the distance from the sun by the inverse square law. However, The geometrical method used by Newton to prove the result is quite complicated. The demonstration below is based on calculus.^[13]

Acceleration vector

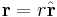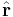From the heliocentric point of view consider the vector to the planet $\mathbf{r} = r \hat{\mathbf{r}}$ where $r$ is the distance to the planet and the direction $\hat {\mathbf{r}}$ is a unit vector. When the planet moves the direction vector 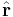$\hat {\mathbf{r}}$ changes:

$\frac{d\hat{\mathbf{r}}}{dt}=\dot{\hat{\mathbf{r}}} = \dot\theta \hat{\boldsymbol\theta},\qquad \dot{\hat{\boldsymbol\theta}} = -\dot\theta \hat{\mathbf{r}}$

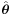where $\scriptstyle \hat{\boldsymbol\theta}$ is the unit vector orthogonal to 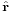$\scriptstyle \hat{\mathbf{r}}$ and pointing in the direction of rotation, and 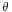$\scriptstyle \theta$ is the polar angle, and where a dot on top of the variable signifies differentiation with respect to time.

So differentiating the position vector twice to obtain the velocity and the acceleration vectors:

$\dot{\mathbf{r}} =\dot{r} \hat{\mathbf{r}} %2B r \dot{\hat{\mathbf{r}}} =\dot{r} \hat{\mathbf{r}} %2B r \dot{\theta} \hat{\boldsymbol{\theta}},$

$\ddot{\mathbf{r}} = (\ddot{r} \hat{\mathbf{r}} %2B\dot{r} \dot{\hat{\mathbf{r}}} ) %2B (\dot{r}\dot{\theta} \hat{\boldsymbol{\theta}} %2B r\ddot{\theta} \hat{\boldsymbol{\theta}} %2B r\dot{\theta} \dot{\hat{\boldsymbol{\theta}}}) = (\ddot{r} - r\dot{\theta}^2) \hat{\mathbf{r}} %2B (r\ddot{\theta} %2B 2\dot{r} \dot{\theta}) \hat{\boldsymbol{\theta}}.$

$\ddot{\mathbf{r}} = a_r \hat{\boldsymbol{r}}%2Ba_\theta\hat{\boldsymbol{\theta}}$

where the radial acceleration is

$a_r=\ddot{r} - r\dot{\theta}^2$

and the tangential acceleration is

$a_\theta=r\ddot{\theta} %2B 2\dot{r} \dot{\theta}.$

The inverse square law

Kepler's second law implies that the areal velocity 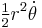$\tfrac 1 2 r^2 \dot \theta$ is a constant of motion. The tangential acceleration 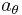$a_\theta$ is zero by Kepler's second law:

$\frac{d (r^2 \dot \theta)}{dt} = r (2 \dot r \dot \theta %2B r \ddot \theta ) = r a_\theta = 0.$

So the acceleration of a planet obeying Kepler's second law is directed exactly towards the sun.

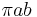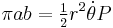Kepler's first law implies that the area enclosed by the orbit is $\pi ab$ , where $a$ is the semi-major axis and $b$ is the semi-minor axis of the ellipse. Therefore the period $P$ satisfies $\pi ab=\tfrac 1 2 r^2\dot \theta P$ or

$r^2\dot \theta = nab$

where

$n = \frac{2\pi}{P}$

is the mean motion of the planet around the sun.

The radial acceleration 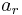$a_r$ is

$a_r = \ddot r - r \dot \theta^2= \ddot r - r \left(\frac{nab}{r^2} \right)^2= \ddot r -\frac{n^2a^2b^2}{r^3}.$

Kepler's first law states that the orbit is described by the equation:

$\frac{p}{r} = 1%2B \varepsilon \cos\theta$

Differentiating with respect to time

$-\frac{p\dot r}{r^2} = -\varepsilon \sin \theta \,\dot \theta$

$p\dot r = nab\,\varepsilon\sin \theta.$

Differentiating once more

$p\ddot r =nab \varepsilon \cos \theta \,\dot \theta =nab \varepsilon \cos \theta \,\frac{nab}{r^2} =\frac{n^2a^2b^2}{r^2}\varepsilon \cos \theta .$

The radial acceleration 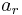$a_r$ satisfies

$p a_r = \frac{n^2 a^2b^2}{r^2}\varepsilon \cos \theta - p\frac{n^2 a^2b^2}{r^3} = \frac{n^2a^2b^2}{r^2}\left(\varepsilon \cos \theta - \frac{p}{r}\right).$

Substituting the equation of the ellipse gives

$p a_r = \frac{n^2a^2b^2}{r^2}\left(\frac p r - 1 - \frac p r\right)= -\frac{n^2a^2}{r^2}b^2.$

The relation 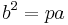$b^2=pa$ gives the simple final result

$a_r=-\frac{n^2a^3}{r^2}.$

This means that the acceleration vector 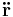$\mathbf{\ddot r}$ of any planet obeying Kepler's first and second law satisfies the inverse square law

$\mathbf{\ddot r} = - \frac{\alpha}{r^2}\hat{\mathbf{r}}$

where

$\alpha = n^2 a^3=\frac{4\pi^2 a^3}{P^2}\,$

is a constant, and 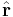$\hat{\mathbf r}$ is the unit vector pointing from the Sun towards the planet, and 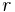$r\,$ is the distance between the planet and the Sun.

According to Kepler's third law, $\alpha$ has the same value for all the planets. So the inverse square law for planetary accelerations applies throughout the entire solar system.

The inverse square law is a differential equation. The solutions to this differential equation includes the Keplerian motions, as shown, but they also include motions where the orbit is a hyperbola or parabola or a straight line. See kepler orbit.

Newton's law of gravitation

By Newton's second law, the gravitational force that acts on the planet is:

$\mathbf{F} = m \mathbf{\ddot r} = - \frac{m \alpha}{r^2}\hat{\mathbf{r}}$

where $\alpha$ only depends on the property of the Sun. According to Newton's third Law, the Sun is also attracted by the planet with a force of the same magnitude. Now that the force is proportional to the mass of the planet, under the symmetric consideration, it should also be proportional to the mass of the Sun. So the form of the gravitational force should be

$\mathbf{F} = - \frac{GMm}{r^2}\hat{\mathbf{r}}$

where $G$ is a universal constant. This is Newton's law of universal gravitation.

The acceleration of solar system body no i is, according to Newton's laws:

$\mathbf{\ddot r_i} = G\sum_{j\ne i} \frac{m_j}{r_{ij}^2}\hat{\mathbf{r}}_{ij}$

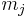where $m_j$ is the mass of body no j, and 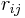$r_{ij}$ is the distance between body i and body j, and 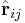$\hat{\mathbf{r}}_{ij}$ is the unit vector from body i pointing towards body j, and the vector summation is over all bodies in the world, besides no i itself. In the special case where there are only two bodies in the world, Planet and Sun, the acceleration becomes

$\mathbf{\ddot r}_{Planet} = G\frac{m_{Sun}}{r_{{Planet},{Sun}}^2}\hat{\mathbf{r}}_{{Planet},{Sun}}$

which is the acceleration of the Kepler motion.

Notes

^ ^a ^b Bryant, Jeff; Pavlyk, Oleksandr. "Kepler's Second Law", Wolfram Demonstrations Project. Retrieved December 27, 2009.
^ ^a ^b ^c Holton, Gerald James; Brush, Stephen G. (2001). Physics, the Human Adventure: From Copernicus to Einstein and Beyond (3rd paperback ed.). Piscataway, NJ: Rutgers University Press. pp. 40–41. ISBN 0-8135-2908-5. http://books.google.com/?id=czaGZzR0XOUC&pg=PA40. Retrieved December 27, 2009.
^ ^a ^b ^c See also G E Smith, "Newton's Philosophiae Naturalis Principia Mathematica", especially the section Historical context ... in The Stanford Encyclopedia of Philosophy (Winter 2008 Edition), Edward N. Zalta (ed.).
^ ^a ^b Newton's showing, in the 'Principia', that the two-body problem with centripetal forces results in motion in one of the conic sections, is concluded at Book 1, Proposition 13, Corollary 1. His consideration of the effects of perturbations in a multi-body situation starts at Book 1, Proposition 65, including a limit argument that the error in the (Keplerian) approximation of ellipses and equal areas would tend to zero if the relevant planetary masses would tend to zero and with them the planetary mutual perturbations (Proposition 65, Case 1). He discusses the extent of the perturbations in the real solar system in Book 3, Proposition 13.
^ Kepler "for the first time revealed" a "real approximation to the true kinematical relations [motions] of the solar system", see page 1 in H C Plummer (1918), An introductory treatise on dynamical astronomy, Cambridge, 1918.
^ Wilson, Curtis (May 1994). "Kepler's Laws, So-Called". HAD News (Washington, DC: Historical Astronomy Division, American Astronomical Society) (31): 1–2. http://had.aas.org/hadnews/HADN31.pdf. Retrieved December 27, 2009.
^ Dunbar, Brian (2008). SECCHI Makes a Fantastic Recovery!. NASA. http://erc.ivv.nasa.gov/mission_pages/stereo/news/SECCHI_P2003.html
^ Gerald James Holton, Stephen G. Brush (2001). Physics, the Human Adventure. Rutgers University Press. p. 45. ISBN 0813529085. http://books.google.com/?id=czaGZzR0XOUC&pg=PA45&dq=Kepler+%22harmonic+law%22.
^ Burtt, Edwin. The Metaphysical Foundations of Modern Physical Science. p. 52.
^ http://www.astro.lsa.umich.edu/undergrad/Labs/extrasolar_planets/pn_intro.html
^ Astronomical Almanac for 2008, page K7.
^ The fact was already stated by Newton ('Principia', Book 3, Proposition 12).
^ Hai-Chau Chang, Wu-Yi Hsiang. "The epic journey from Kepler's laws to Newton's law of universal gravitation revisited". arXiv:0801.0308.

References

Kepler's life is summarized on pages 523–627 and Book Five of his magnum opus, Harmonice Mundi (harmonies of the world), is reprinted on pages 635–732 of On the Shoulders of Giants: The Great Works of Physics and Astronomy (works by Copernicus, Kepler, Galileo, Newton, and Einstein). Stephen Hawking, ed. 2002 ISBN 0-7624-1348-4

A derivation of Kepler's third law of planetary motion is a standard topic in engineering mechanics classes. See, for example, pages 161–164 of Meriam, J. L. (1966, 1971). Dynamics, 2nd ed. New York: John Wiley. ISBN 0-471-59601-9 .

Murray and Dermott, Solar System Dynamics, Cambridge University Press 1999, ISBN 0-521-57597-4
V.I. Arnold, Mathematical Methods of Classical Mechanics, Chapter 2. Springer 1989, ISBN 0-387-96890-3

External links

B.Surendranath Reddy; animation of Kepler's laws: applet
Crowell, Benjamin, Conservation Laws, http://www.lightandmatter.com/area1book2.html, an online book that gives a proof of the first law without the use of calculus. (see section 5.2, p. 112)
David McNamara and Gianfranco Vidali, Kepler's Second Law - Java Interactive Tutorial, http://www.phy.syr.edu/courses/java/mc_html/kepler.html, an interactive Java applet that aids in the understanding of Kepler's Second Law.
Audio - Cain/Gay (2010) Astronomy Cast Johannes Kepler and His Laws of Planetary Motion
University of Tennessee's Dept. Physics & Astronomy: Astronomy 161 page on Johannes Kepler: The Laws of Planetary Motion [3]
Equant compared to Kepler: interactive model [4]
Kepler's Third Law:interactive model [5]
Solar System Simulator (Interactive Applet)
Kepler and His Laws, educational web pages by David P. Stern

Orbits

General	Box Capture Circular Elliptical / Highly elliptical Escape Graveyard Hyperbolic trajectory Inclined / Non-inclined Osculating Parabolic trajectory Parking Synchronous (semi sub)

Geocentric	Geosynchronous Geostationary Sun-synchronous Low Earth Medium Earth High Earth Molniya Near-equatorial Orbit of the Moon Polar Tundra Two-line elements

About other points	Areosynchronous Areostationary Halo Lissajous Lunar Heliocentric Heliosynchronous

Parameters

Classical	$i\,\!$ Inclination $\Omega\,\!$ Longitude of the ascending node $e\,\!$ Eccentricity $\omega\,\!$ Argument of periapsis $a\,\!$ Semi-major axis $M_o\,\!$ Mean anomaly at epoch

Other	$\nu\,\!$ True anomaly $b\,\!$ Semi-minor axis $\epsilon\,\!$ Linear eccentricity $E\,\!$ Eccentric anomaly $L\,\!$ Mean longitude $l\,\!$ True longitude $T\,\!$ Orbital period

Maneuvers

Bi-elliptic transfer Delta-v budget Geostationary transfer Gravity assist Gravity turn Hohmann transfer Low energy transfer Oberth effect Inclination change Phasing Rendezvous Transposition, docking, and extraction Collision avoidance (spacecraft)

Other orbital mechanics topics

Apsis Celestial coordinate system Characteristic energy Direct motion Epoch Ephemeris Equatorial coordinate system Ground track Interplanetary Transport Network Kepler's laws of planetary motion Lagrangian point n-body problem Orbit equation Orbital speed Orbital state vectors Perturbation Retrograde motion Specific orbital energy Specific relative angular momentum

List of orbits

Kepler's laws of planetary motion

Contents

History

First Law

Second law

Third law

Generality

Zero eccentricity

Relation to Newton's laws

Computing position as a function of time

Mean anomaly, M

Eccentric anomaly, E

True anomaly, θ

Distance, r

Computing the planetary acceleration

Acceleration vector

The inverse square law

Newton's law of gravitation

See also

Notes

References

External links